문제 링크
https://www.acmicpc.net/problem/2609
2609번: 최대공약수와 최소공배수
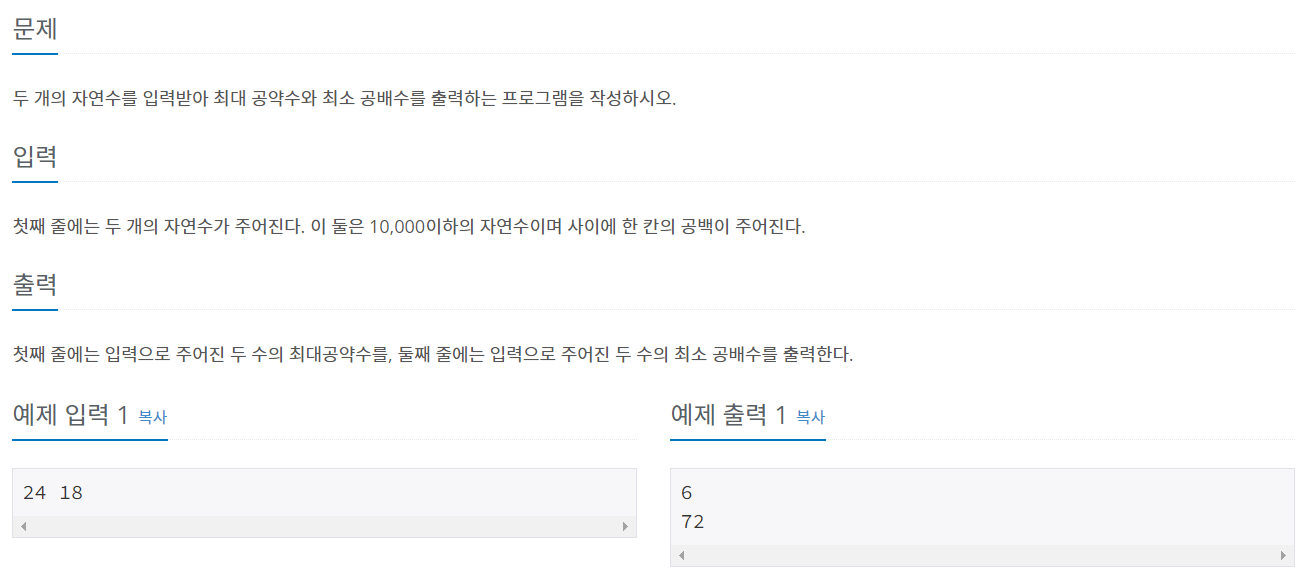
첫째 줄에는 입력으로 주어진 두 수의 최대공약수를, 둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.
www.acmicpc.net
문제
문제 풀이
유클리드 호제법을 이용하는 문제이다.
유클리드 호제법에서는
숫자 a, b가 있을 때, a를 b로 나눈 나머지와 b의 최대 공약수가 a와 b의 최대공약수
와 같다.기존 b를 a에 / a를 b로 나누어 나온 나머지를 b에 대입하는 과정을 반복하여b가 0이 나올 경우 a가 최대공약수가 된다.
예)(18, 12) => (12, 6) => (6, 0)b가 0이 되는 a값은 6이므로 6이 18과 12의 최대공약수가 된다.
최소공배수는 a, b의 곱을 a, b의 최대 공약수로 나누면 나오게 된다.
=> a * b / gcd(a, b)
A, B = map(int, input().split())
a, b = A, B
while b != 0:
a = a % b
a, b = b, a
# gcd
print(a)
#lcm
print(A*B//a)'Algorithm > BOJ' 카테고리의 다른 글
| [백준] 1850 최대공약수 (파이썬 python) (0) | 2022.01.25 |
|---|---|
| [백준] 1934 최소공배수 (파이썬 python) (0) | 2022.01.25 |
| [백준] 10430 나머지 (파이썬 python) (0) | 2022.01.25 |
| [백준] 1158 요세푸스 문제 (파이썬 python) (0) | 2022.01.25 |
| [백준] 10824 네 수 (파이썬 python) (0) | 2022.01.24 |
문제 링크
https://www.acmicpc.net/problem/2609
2609번: 최대공약수와 최소공배수
첫째 줄에는 입력으로 주어진 두 수의 최대공약수를, 둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.
www.acmicpc.net
문제

문제 풀이
유클리드 호제법을 이용하는 문제이다.
유클리드 호제법에서는
숫자 a, b가 있을 때, a를 b로 나눈 나머지와 b의 최대 공약수가 a와 b의 최대공약수
와 같다.기존 b를 a에 / a를 b로 나누어 나온 나머지를 b에 대입하는 과정을 반복하여b가 0이 나올 경우 a가 최대공약수가 된다.
예)(18, 12) => (12, 6) => (6, 0)b가 0이 되는 a값은 6이므로 6이 18과 12의 최대공약수가 된다.
최소공배수는 a, b의 곱을 a, b의 최대 공약수로 나누면 나오게 된다.
=> a * b / gcd(a, b)
A, B = map(int, input().split())
a, b = A, B
while b != 0:
a = a % b
a, b = b, a
# gcd
print(a)
#lcm
print(A*B//a)'Algorithm > BOJ' 카테고리의 다른 글
| [백준] 1850 최대공약수 (파이썬 python) (0) | 2022.01.25 |
|---|---|
| [백준] 1934 최소공배수 (파이썬 python) (0) | 2022.01.25 |
| [백준] 10430 나머지 (파이썬 python) (0) | 2022.01.25 |
| [백준] 1158 요세푸스 문제 (파이썬 python) (0) | 2022.01.25 |
| [백준] 10824 네 수 (파이썬 python) (0) | 2022.01.24 |
